Matrix Algebra

Definitions

Real-valued matrix: a rectangular array of real numbers (same for interger-valued, complex-valued etc.) Matrix size: $m\times n$ , or $m$ by $n$ matrix has $m$ rows and $n$ columns $a_{ij}$ or the $(i,j)$ -entry refers to the entry in row $i$ and column $j$

Representing Matrices

A matrix can be defined by a formula on its entry, e.g. $A=(a_{ij}{)}_{2\times 3},a_{ij}=i+j$ represents a 2 by 3 matrix where the $(i,j)$ -entry is $i+j$

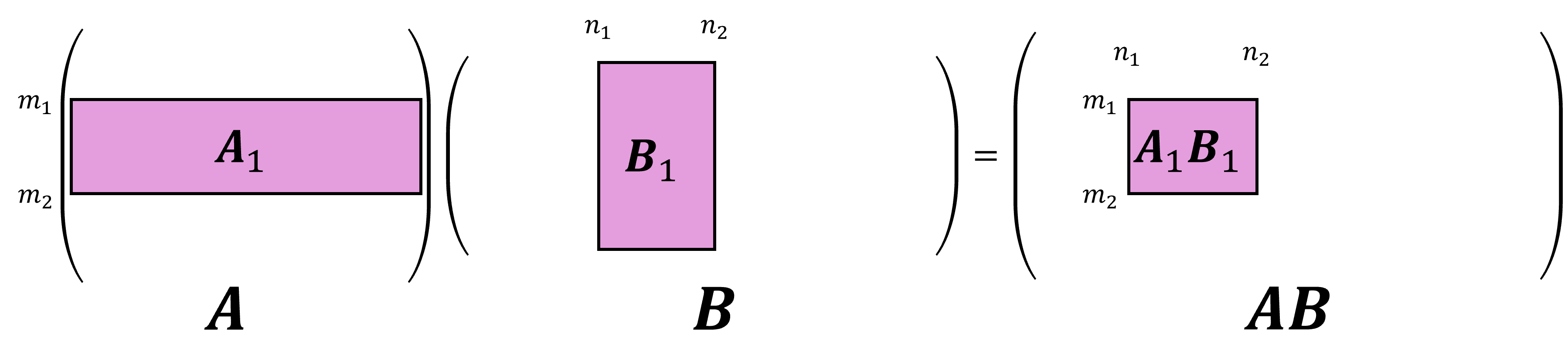
Submatrix

• A $p\times q$ submatrix of an $m\times n$ matrix $A$, with $p\le m,q\le n$ is formed by taking a $p\times q$ block of the entries of the matrix $A$
• Block multiplication:

Special Types of Matrices

• Vectors: a $n\times 1$ matrix is a (column) vector, and a $1\times n$ matrix is a (row) vector. By default, a vector is a column vector
• Zero matrix: All entries are zero, denoted $0_{m\times n}$
• Square matrix: It has the same number of rows and columns, a $n\times n$ matrix is a square matrix of order $n$
• Diagonal matrix: All entries not along the diagonals are zero, can be denoted as $\text{diag}(d_1,d_2,\dots ,d_n)$ , where $d_n$ is the $(n,n)$ -entry
• Scalar matrix: A diagonal matrix where all the diagonals are the same constant: $\text{diag}(c,c,\dots ,c)$
• Identity matrix: A scalar matrix where the constant is 1: $\text{diag}(1,1,\dots ,1)$
• Upper triangular matrix: square matrix where all values below the diagonal (not including the diagonal) are zero
• Strictly upper triangular matrix: upper triangular matrix, but all values on the diagonal are also zero
• Lower/Strictly lower triangular matrix: same as upper
• Symmetric matrix: the ij entry is equal to the ji entry (the matrix is reflected about the diagonal) ($A=A^T$)

Operations

Scalar multiplication & Addition

• Scalar multiplication: Multiply each element in the matrix by the scalar value
• Addition: Add each corresponding element together
• Properties for $m\times n$ matrices $A$ , $B$ and $C$
  • Commutative $A+B=B+A$
  • Associative $A+(B+C)=(A+B)+C$
  • Additive identity $0_{m\times n}+A=A$
  • Additive inverse $A+(-A)=0_{m\times n}$
  • Distributive $a(A+B)=aA+aB$
  • Scalar addition $(a+b)A=aA+bA$
  • Associative $(ab)A=a(bA)$
  • if $aA=0_{m\times n}$ , then either $a=0$ or $A=0$

Matrix Multiplication

• $AB=(a_{ij}{)}_{m\times p}(b_{ij}{)}_{p\times n}=({\sum }_{k=1}^p{a}_{ik}{b}_{kj}{)}_{m\times n}$
• $A$ is pre-multiplied to $B$ means $AB$
• $A$ is post-multiplied to $B$ means $BA$
• Properties for matrices with sizes for the operations to be well defined
  • Not commutative $AB\ne BA$
  • Associative: $(AB)C=A(BC)$
  • Left distributive law: $A(B+C)=AB+AC$
  • Right distributive law: $(A+B)C=AC+BC$
  • Commute with scalar multiplication: $c(AB)=(cA)B=A(cB)$
  • Multiplicative identity: for $m\times n$ matrix $A$ , $I_{m}A=A=A{I}_n$
  • Nonzero zero divisor: There exists $A\ne 0_{m\times p}$ and $B\ne 0_{m\times p}$ such that $AB=0_{m\times n}$
  • Zero matrix: $A0=0$ and $0A=0$

Power

• Power can only be applied to square matrices, defined as:
  • $A^0=I$ (identity)
  • $A^n=A{A}^{n-1}$ , for $n\ge 1$

Transpose

• Transpose of matrix $A$, or $A^T$ , is a matrix where the $ij$ entry of $A^T$ is the $ji$ entry of $A$
• Write the rows as columns or columns as rows (first row of $A$ is first column of $A^T$)
• Properties
  • $(A^T{)}^T=A$
  • $(cA{)}^T=c{A}^T$
  • $(A+B{)}^T=A^T+B^T$
  • $(AB{)}^T=B^T{A}^T$ , or $(A_1{A}_2\cdots A_k{)}^T=A_k^T\cdots A_2^T{A}_1^T$

Elementary Row Operations

• Exchanging two rows: $R_i\leftrightarrow Rj$
• Adding a multiple of a row to another $R_i+c{R}_j,c\in \mathbb{R},i\ne j$
• Multiplying a row by a nonzero constant $a{R}_j,a\ne 0$
• An elementary matrix is a square matrix that corresponds to an elementary row operation. Pre-multiplying a matrix by an elementary matrix is the same as performing the elementary row operation
  • Obtained by performing the corresponding row operation to the identity matrix
  • Inverse of elementary matrix is reverse row operation
• Two augmented matrices are row equivalent if one can be obtained from the other by elementary row operations
  • Two linear systems have the same solution if their augmented matrices are row equivalent
  • This means that we can solve a linear system by converting it to REF by performing elementary row operations

Inverse

• Inverse of a square matrix $A$ is $B$ , then $AB=I=BA$
• Inverse is denoted $A^{-1}$
• A matrix is invertible if its inverse exists. Otherwise, it is non-invertible
• A non-invertible square matrix is called a singular matrix
• The inverse of a matrix is inverse
• A $2\times 2$ matrix $\mathbf{A}=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$ is invertible iff $ad-bc\ne 0$ ${\mathbf{A}}^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$
• Finding inverse of any matrix: $\left(\begin{array}{c}\mathbf{A}\mid \mathbf{I}\end{array}\right)\stackrel{RREF}{\to }\left(\begin{array}{c}\mathbf{I}\mid {\mathbf{A}}^{-1}\end{array}\right)$
  • If after RREF, the left side is not identity matrix, then the matrix is not invertible
• These statements are equivalent, for square matrix $A$
  • $A$ is invertible
  • $A^T$ is invertible
  • $A$ has a left-inverse: $BA=I$
  • $A$ has a right-inverse: $AB=I$
  • The RREF of $A$ is $I$
  • $A$ can be expressed as a product of elementary matrices
  • Homogeneous system $Ax=0$ only has trivial solution
  • For any $b$, the system $Ax=b$ is consistent
• Properties (let $A$ be order n invertible matrix)
  • $(A^{-1}{)}^{-1}=A$
  • For nonzero real number $a$ , $aA$ is invertible with inverse $\frac{1}{a}{A}^{-1}$
  • $A^T$ is invertible with inverse $(A^{-1}{)}^T$
  • if $B$ is order n invertible matrix, then $AB$ is invertible, with inverse

LU Factorisation

1. Turn matrix into REF
2. Write the elementary matrices corresponding to the operations to get REF (U matrix)
   1. $E_k\dots E_2{E}_{1}A=U\Rightarrow A=(E_1^{-1}{E}_2^{-1}...)U=LU$

To solve Linear system:

1. For the system $Ax=b$ , let $A=LU$
2. $LUx=b$, let $Ux=y$ , so $L(Ux)=Ly=b$
3. Solve $Ux=y$ , then solve $Ly=b$