Properties of Set Relations

Properties of Set Relations Note: These are properties of relations, not elements of sets (“element 0 is reflexive” is wrong, “the relation $R$ is reflexive”)

Reflexive

Definition

$R$ is reflexive iff all elements in the set are related to themselves $\forall x\in A(xRx)$

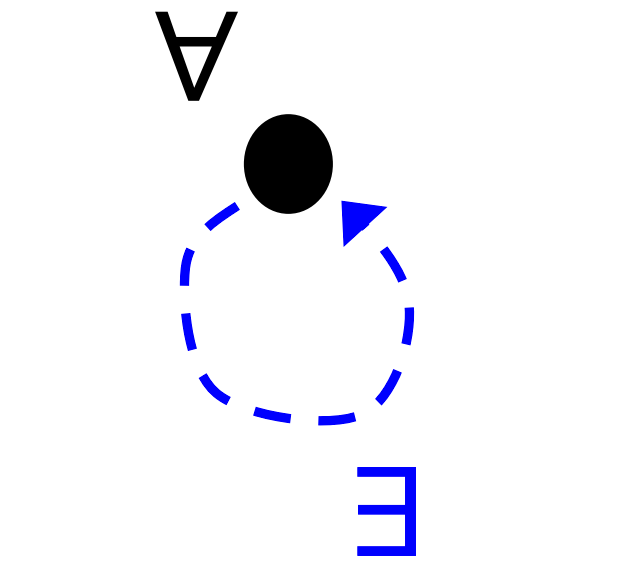
Symmetric

Definition

$R$ is symmetric iff for all elements $x$ that is related to $y$, $y$ is also related to $x$ $\forall x,y\in A(xRy\Rightarrow yRx)$

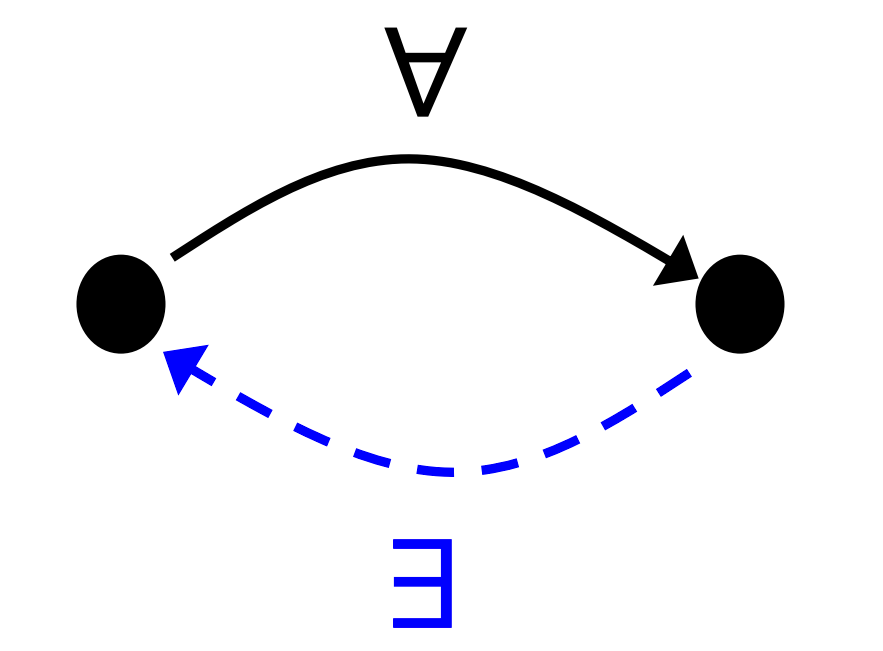
Not Symmetric

Negation of definition of symmetric $\exists x,y\in A(xRy\wedge y/Rx)$

Antisymmetric

There does not exist elements $x,y$ where $x\ne y$ $x$ is related to $y$ and $y$ is related to $x$ Let $R$ be a relation on set $A$. $R$ is antisymmetric iff $\forall x,y\in A(xRy\wedge yRx\Rightarrow x=y)$

Different from not symmetric

• Not symmetric
  • At least one pair of elements is only related one way
• Asymmetric
  • Not a single pair of elements are related “two-way”, including two of the same element (i.e. no element is related to itself)
• Antisymmetric
  • Not a single pair of elements are related “two-way”

Asymmetric

$\forall x,y\in A(xRy\Rightarrow y/Rx)$

Transitive

Definition

$R$ is transitive iff for all elements $x$ that is related to $y$, and $y$ is related to $z$, $x$ is related to $z$ $\forall x,y,z\in A(xRy\wedge yRz\Rightarrow xRz)$

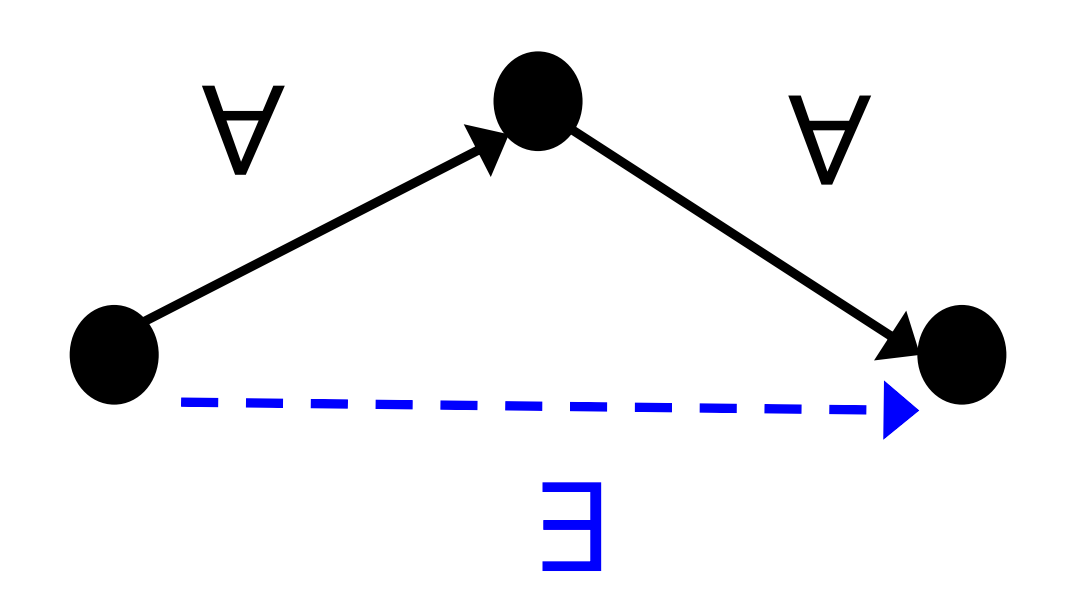
Transitive Closure

The transitive closure of a relation $R$, denoted as $R^t$, is the smallest superset of $R$ that is transitive i.e. To find $R^t$, add the least number of arrows to the directed graph of $R$ to make it transitive Note: when trying to find the transitive closure, keep checking for transitivity after each round of adding arrows Formally, it satisfies all the following:

1. $R^t$ is transitive
2. $R\subseteq R^t$
3. If $S$ is any other transitive relation that contains $R$ ($R\subseteq S$), then $R^t\subseteq S$
   • This means that $R^t$ is the smallest possible relation that is transitive

Example

Set Relation Properties 2024-10-04 02.56.54.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠ You can decompress Drawing data with the command palette: ‘Decompress current Excalidraw file’. For more info check in plugin settings under ‘Saving’

Excalidraw Data

Text Elements

Embedded Files

cbab65d6da187952222c5b0a286ec6ae3bf5e847: $R$

1e4bb51a12f788d49cec5e422dae640587999f05: $R^t$

95c5e3e3e5745bb8853e43e00feaabf3653d520d: image_1.png

4dbe37140d70d8134521bd5e2738f6238f412955: image_2.png

Link to original

Relation Induced by a Partition

Given a partition $\mathcal{C}$ of a set $A$, the relation $R$ induced by the partition is defined on $A$ as: $\forall x,y\in A$, $xRy\iff \exists$ a component $S$ of $\mathcal{C}$ such that $x,y\in S$ A partition is the same as an Equivalence Relations, but from different perspectives.

Properties

A relation induced by a partition is reflexive, symmetric and transitive

Example

Let set $A=\{0,1,2,3,4\}$ Let partition of the set $\mathcal{C}=\left\{\{0,1,2\},\{3\},\{4\}\right\}$ Relation induced by the partition is: $0R0,0R1,0R2,1R0,1R1,1R2,2R0,2R1,2R2,3R3,4R4$