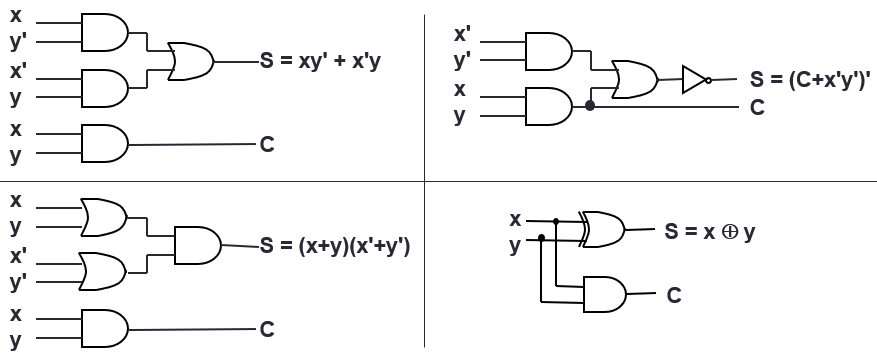Gate-level design

Determine inputs/outputs
Truth table
Simplify (can use k-maps)
Implement using logic gates

Examples

Half Adder

X	Y	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

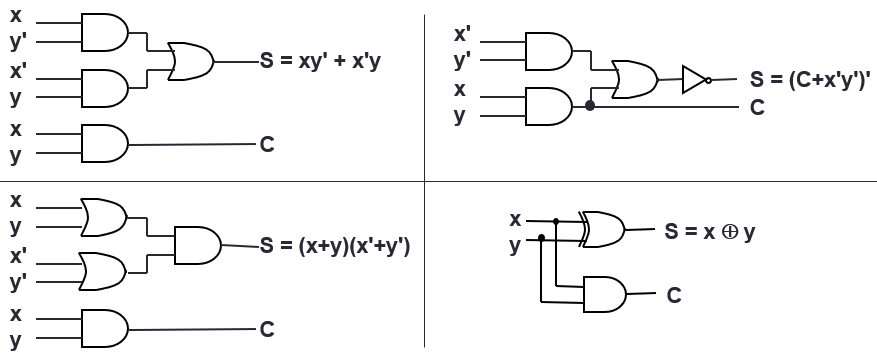
Full Adder

A	B	Cin	Cout	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

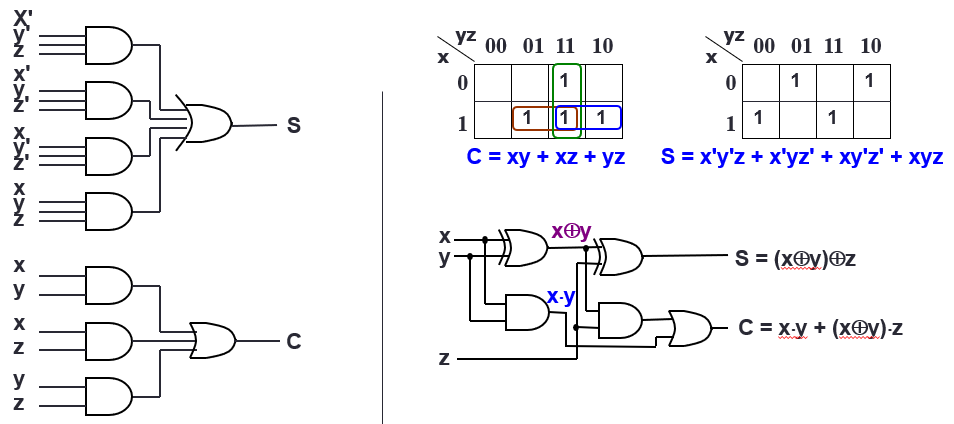
Block-level design

MSI Components (med scale integration)

Decoder

Based on the input bits, the decoder makes one of the outputs high
n-bit decoder can have up to $2^{n}$ outputs
Any combinational circuit with n inputs and m outputs can be implemented with an $n : 2^{n}$ decoder with m OR gates.
Use when circuit has many outputs, and each function is expressed with a few minterms
- Use decoder to generate minterms, then OR gates to form the sum

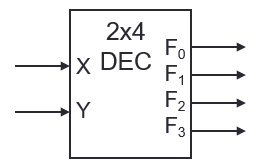
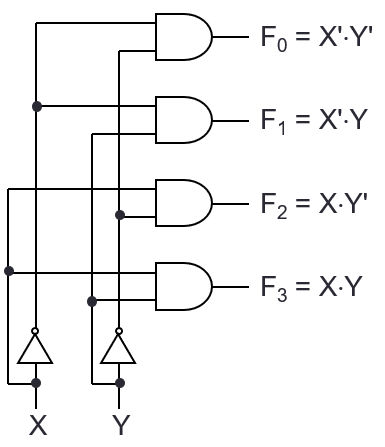
$X$	$Y$	$F_{0}$	$F_{1}$	$F_{2}$	$F_{3}$
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Encoder

Based on up to $2^{n}$ input bits (of which exactly one is high), encode to n outputs

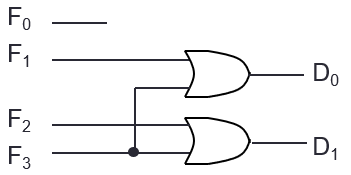
$F_{0}$	$F_{1}$	$F_{2}$	$F_{3}$	$D_{1}$	$D_{0}$
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1
the	rest			X	X

Priority Encoder

If more than one input is high, take the highest priority one
If all inputs are zero, it is invalid (V=0)

$F_{0}$	$F_{1}$	$F_{2}$	$F_{3}$	$D_{1}$	$D_{0}$	$V$
0	0	0	0	X	X	0
1	0	0	0	0	0	1
X	1	0	0	0	1	1
X	X	1	0	1	0	1
X	X	X	1	1	1	1

Demultiplexer

Depending on the input from select lines, data is “routed” to one of the outputs
Identical to a decoder with enable

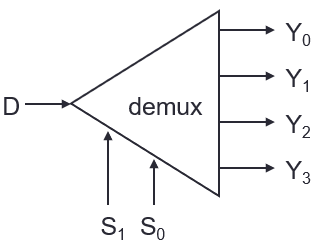
$S_{1}$	$S_{0}$	$Y_{0}$	$Y_{1}$	$Y_{2}$	$Y_{3}$
0	0	D	0	0	0
0	1	0	D	0	0
1	0	0	0	D	0
1	1	0	0	0	D

Multiplexer

“routes” one of up to $2^{n}$ input bits to one output bit
Multiplexers can be combined to make bigger multiplexer (e.g. 2 4-bit multiplexers combined using one 2-bit multiplexer)
Implementing a function with n-bit input
- n-bit ( $2^{n}$ to one) multiplexer: put 1 on the input if the minterm is 1, 0 otherwise
- (n-1)-bit multiplexer: put either 1, 0, A or A’ where A is the last input bit

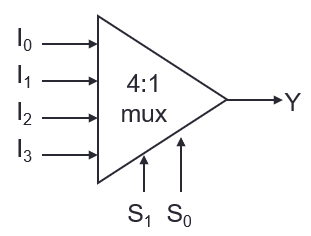
$S_{1}$	$S_{0}$	$Y$
0	0	$I_{0}$
0	1	$I_{1}$
1	0	$I_{2}$
1	1	$I_{3}$

Calculating Delay

Consider a logic gate with delay t. The time that the outputs become stable is the latest time the input becomes stable + t