Relations

Relation (between two sets)

Let $A$ and $B$ be sets, a binary relation from $A$ to $B$ is a subset of $A\times B$. Given an ordered pair $(x,y)$ in $A\times B$, $x$ is related to $y$ by $R$, or $x$ is $R$-related to $y$.

Relation on a Set

A relation on set $A$ is a relation from $A$ to $A$ It is a subset of $A\times A$ ($A^2$) Note: the arrow diagram of such a relation can be modified so that it becomes a directed graph

Notation

$x$ is related to $y$ by $R$ $xRy$ means $(x,y)\in R$ $x/Ry$ means $(x,y)\notin R$

Domain, Co-domain, Range

Let $A$ and $B$ be sets and $R$ be a relation from $A$ to $B$

Domain

$Dom(R)$ is the set $\{a\in A:aRb\text{ for some }b\in B\}$

Elements in $B$ that are “part of” $R$

Co-domain

$coDom(R)$ is the set $B$

Range

$Range(R)$ is the set $\{b\in B:aRb\text{ for some }a\in A\}$

Elements in A that are “part of” $R$

Inverse Relation

If $R$ is a relation from $A$ to $B$, then a relation $R^{-1}$ from $B$ to $A$ can be defined by interchanging the elements of all the ordered pairs of $R$ Either $R^{-1}=\{(y,x)\in B\times A:(x,y)\in R\}$ Or $\forall x\in A,\forall y\in B\left((y,x)\in R^{-1}\iff (x,y)\in R\right)$

N-ary Relations

A $n$-ary relation involves $n$ sets. Given $n$ sets $A_1,A_2,\dots ,A_n$, an $n$-are relation $R$ on $A_1\times A_2\times \cdots \times A_n$ is a subset of $A_1\times A_2\times \cdots \times A_n$ 2-ary, 3-ary and 4-ary relations are called binary, ternary and quatenary relations respectively

Examples

1: Relation

Let $A=\{0,1,2\}$ and $B=\{1,2,3\}$ Suppose we define the relation R such that $xRy$ iff $x<y$ Then, $0R1,0R2,0R3,1R2,1R3,2R3$ but $1/R1,2/R1,2/R2$

2: Defining Relations

Let $A=\{1,2\}$ and $B=\{1,2,3\}$ Relation $R$ is defined from $A$ to $B$ as: $\forall (x,y)\in A\times B\left((x,y)\in R\iff \frac{x-y}{2}\in \mathbb{Z}\right)$ State explicitly which ordered pairs are in $A\times B$ and which are in $R$ $A\times B=\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)\}$ $R=\{(1,1),(1,3),(2,2)\}$

3: Domain, Co-domain, Range

Let $A=\{1,2,3\}$ and $B=\{2,4,9\}$, and define a relation $R$ from $A$ to $B$ as follows: $\forall (x,y)\in A\times B,(x,y)\in R\iff x^2=y$ $Dom(R)=\{2,3\}$ $coDom(R)=\{2,4,9\}$ $Range(R)=\{4,9\}$

Properties of Relations

Properties of Set Relations Note: These are properties of relations, not elements of sets (“element 0 is reflexive” is wrong, “the relation $R$ is reflexive”)

Reflexive

Definition

$R$ is reflexive iff all elements in the set are related to themselves $\forall x\in A(xRx)$

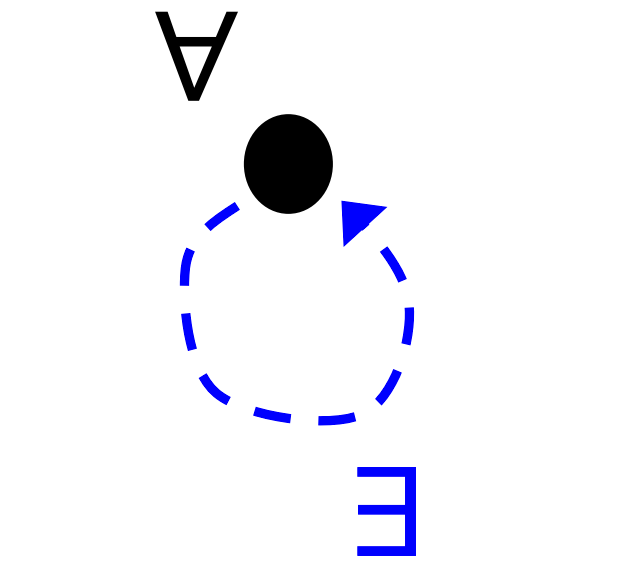
Symmetric

Definition

$R$ is symmetric iff for all elements $x$ that is related to $y$, $y$ is also related to $x$ $\forall x,y\in A(xRy\Rightarrow yRx)$

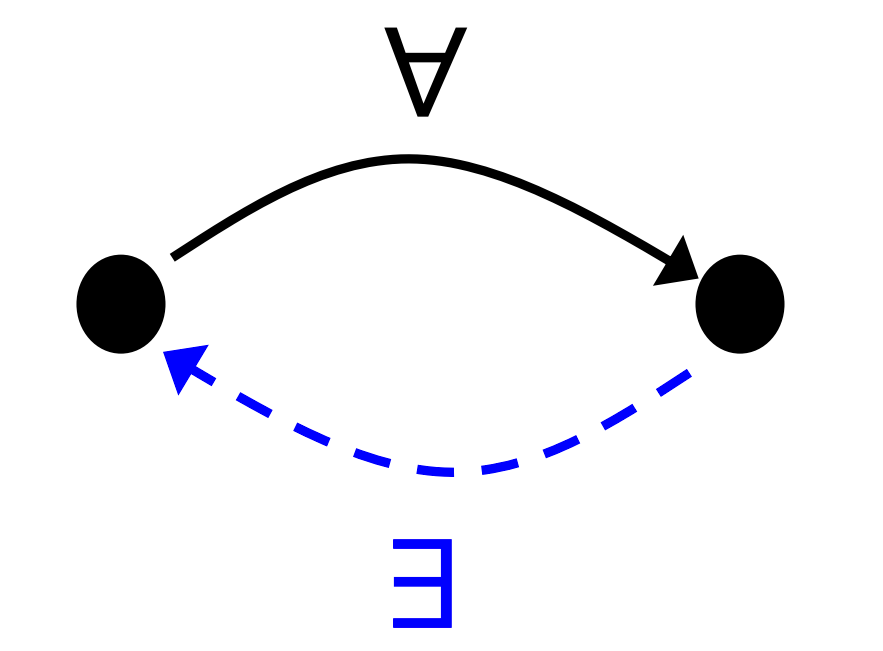
Not Symmetric

Negation of definition of symmetric $\exists x,y\in A(xRy\wedge y/Rx)$

Antisymmetric

There does not exist elements $x,y$ where $x\ne y$ $x$ is related to $y$ and $y$ is related to $x$ Let $R$ be a relation on set $A$. $R$ is antisymmetric iff $\forall x,y\in A(xRy\wedge yRx\Rightarrow x=y)$

Different from not symmetric

• Not symmetric
  • At least one pair of elements is only related one way
• Asymmetric
  • Not a single pair of elements are related “two-way”, including two of the same element (i.e. no element is related to itself)
• Antisymmetric
  • Not a single pair of elements are related “two-way”

Asymmetric

$\forall x,y\in A(xRy\Rightarrow y/Rx)$

Transitive

Definition

$R$ is transitive iff for all elements $x$ that is related to $y$, and $y$ is related to $z$, $x$ is related to $z$ $\forall x,y,z\in A(xRy\wedge yRz\Rightarrow xRz)$

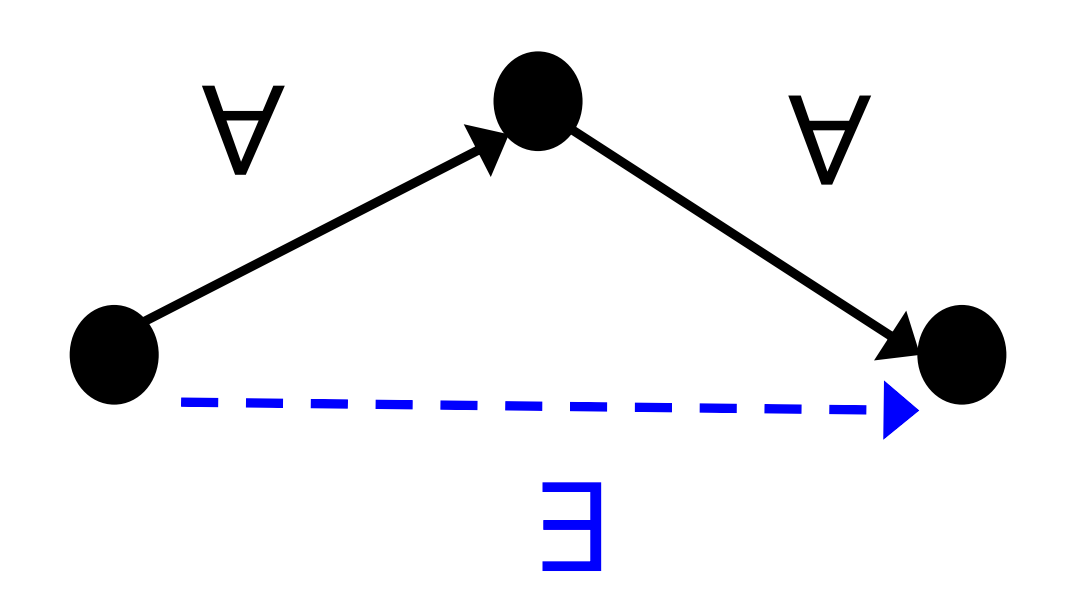
Transitive Closure

The transitive closure of a relation $R$, denoted as $R^t$, is the smallest superset of $R$ that is transitive i.e. To find $R^t$, add the least number of arrows to the directed graph of $R$ to make it transitive Note: when trying to find the transitive closure, keep checking for transitivity after each round of adding arrows Formally, it satisfies all the following:

1. $R^t$ is transitive
2. $R\subseteq R^t$
3. If $S$ is any other transitive relation that contains $R$ ($R\subseteq S$), then $R^t\subseteq S$
   • This means that $R^t$ is the smallest possible relation that is transitive

Example

Set Relation Properties 2024-10-04 02.56.54.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠ You can decompress Drawing data with the command palette: ‘Decompress current Excalidraw file’. For more info check in plugin settings under ‘Saving’

Excalidraw Data

Text Elements

Embedded Files

cbab65d6da187952222c5b0a286ec6ae3bf5e847: $R$

1e4bb51a12f788d49cec5e422dae640587999f05: $R^t$

95c5e3e3e5745bb8853e43e00feaabf3653d520d: image_1.png

4dbe37140d70d8134521bd5e2738f6238f412955: image_2.png

Link to original

Relation Induced by a Partition

Given a partition $\mathcal{C}$ of a set $A$, the relation $R$ induced by the partition is defined on $A$ as: $\forall x,y\in A$, $xRy\iff \exists$ a component $S$ of $\mathcal{C}$ such that $x,y\in S$ A partition is the same as an Equivalence Relations, but from different perspectives.

Properties

A relation induced by a partition is reflexive, symmetric and transitive

Example

Let set $A=\{0,1,2,3,4\}$ Let partition of the set $\mathcal{C}=\left\{\{0,1,2\},\{3\},\{4\}\right\}$ Relation induced by the partition is: $0R0,0R1,0R2,1R0,1R1,1R2,2R0,2R1,2R2,3R3,4R4$

Relation Diagrams

Arrow Diagram

Let $A=\{1,2,3\}$ and $B=\{1,3,5\}$. Define relations $S$ and $T$ from $A$ to $B$ as follows: $\forall (x,y)\in A\times B$, $(x,y)\in S\iff x<y$ $T=\{(2,1),(2,5)\}$

Set Relations 2024-10-03 17.49.49.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠ You can decompress Drawing data with the command palette: ‘Decompress current Excalidraw file’. For more info check in plugin settings under ‘Saving’

Excalidraw Data

Text Elements

1

2

3

1

3

5

S

1

2

3

1

3

5

T

Link to original

Directed Graph

Only for relations on a set. Let $A=\{3,4,5,6\}$, and define $R$ on $A$ as: $\forall x,y\in A,xRy\iff 2|(x-y)$

Set Relations 2024-10-03 20.23.45.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠ You can decompress Drawing data with the command palette: ‘Decompress current Excalidraw file’. For more info check in plugin settings under ‘Saving’

Excalidraw Data

Text Elements

3

4

6

5

Link to original

Relation Composition

Definition

Let $A$, $B$ and $C$ be sets. Let $R\subseteq A\times B$ be a relation, and $S\subseteq B\times C$ be a relation. The composition of $R$ with $S$ ($R\circ S$) is the relation from $A$ to $C$ such that: $\forall x\in A,\forall z\in C\left(xS\circ Rz\iff \left(\exists y\in B(xRy\wedge ySz)\right)\right)$ i.e. $x\in A$ and $z\in C$ are "$S\circ R$" related iff there s a “path” from $x$ to $z$ via some intermediate element $y\in B$ in the arrow diagram

Laws

Let $A$, $B$, $C$ and $D$ be sets. Let $R\subseteq A\times B$, $S\subseteq B\times C$ and $T\subseteq C\times D$ be relations.

Associative

$T\circ (S\circ R)=(T\circ S)\circ R=T\circ S\circ R$

Inverse

$(S\circ R{)}^{-1}=R^{-1}\circ S^{-1}$

Partial Order Relations

Definition

A relation is a partial order relation (or partial order) iff it is reflexive, antisymmetric and transitive. $\preccurlyeq$ is used to denote a partial order relation (it replaces $R$ in $aRb$, so $a\preccurlyeq b$), read ”$a$ is curly less than or equal to $y$“

Partially Ordered Set

A set $A$ is a partially ordered set or poset with respect to a partial order relation $R$ on $A$, denoted by $(A,R)$ A set with a partial order relation defined on it can be represented $(A,R)$ and be called a poset

Hasse Diagram

Partial order relations can be represented as hasse diagrams

1. Start with a directed graph
2. Remove loops on nodes (because reflexive)
3. Arrange nodes such that all arrows are pointing up, then remove arrow heads (because antisymmetric)
4. Remove arrows that are implied by transitivity
   • If there is an arrow from $a$ to $b$ and $b$ to $c$, remove the arrow from $a$ to $c$
   • Keep repeating to remove as many arrows as possible

Example

For the “divides” relation on set $A=\{1,2,3,9,18\}$

Partial Order Relations 2024-10-05 06.21.24.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠ You can decompress Drawing data with the command palette: ‘Decompress current Excalidraw file’. For more info check in plugin settings under ‘Saving’

Excalidraw Data

Text Elements

Directed Graph

Hasse Diagram

Embedded Files

200bb00677aa83342ccef1087c52e673c454aa82: image.png

acb4d4eb3d78d42155a9149398dea983c5eba8d5: image_0.png

Link to original

Formal Definition

Let $\preccurlyeq$ be a partial order on a set $A$. A Hasse diagram of $\preccurlyeq$ satisfies the following condition for all distinct $x,y,m\in A$: If $x\preccurlyeq y$ and no $m\in A$ is such that $x\preccurlyeq m\preccurlyeq y$, then $x$ is placed below $y$ with a line joining them, else no line joins $x$ and $y$

Analogy

Putting on socks and shoes (ignore reflexivity)

• left sock must go on before left shoe, same for right
• but whether the left or right sock goes on first does not matter
• whether the left shoe goes on before the right sock does not matter
• left sock $\preccurlyeq$ left shoe
• right sock $\preccurlyeq$ right shoe
• the order is “partial” because there may not be an order between certain elements
• left sock and right sock are not comparable

Common Examples

• The “divides” relation, $|$, on a set of positive integers
• $\le$ on a set of real numbers
• $\subseteq$ on a set of sets

Properties of Poset Elements

Suppose $\preccurlyeq$ is a partial order relation on a set $A$ For example, the hasse diagram of $|$ on $A=\{1,2,\dots ,10\}$

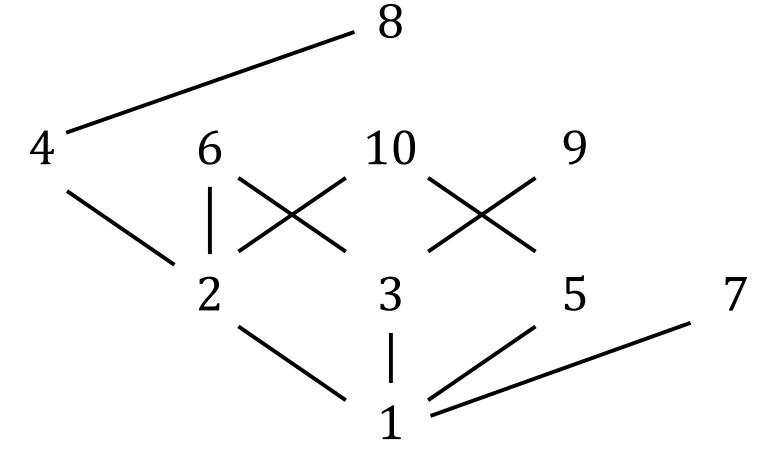
Comparability

Elements $a$ and $b$ of $A$ are said to be comparable iff either $a\preccurlyeq b$ or $b\preccurlyeq a$. Otherwise, $a$ and $b$ are noncomparable Hasse diagram: Comparable means having a path between the elements that only goes up In the example $2$ and $8$ are comparable, but $5$ and $9$ are not

Compatibility

Elements $a$ and $b$ of $A$ are said to be compatible iff there exists $c\in A$ such that $a\preccurlyeq c$ and $b\preccurlyeq c$
Hasse diagram: The elements have have a path upwards to the same elements
In the example, $1$ and $8$ , $2$ and $3$ are compatible but $3$ and $5$ are not

Maximal Element

Element $c$ of $A$ is a maximal element of $A$ iff $\forall x\in A$, either $x\preccurlyeq c$ or $x$ and $c$ are noncomparable $\forall x\in A(c\preccurlyeq x\Rightarrow c=x)$ Hasse diagram: There are no lines upward from the element In the example $6,7,8,9,10$ are the maximal elements

Minimal Element

Element $c$ of $A$ is a minimal element of $A$ iff $\forall x\in A$, either $c\preccurlyeq x$ or $x$ and $c$ are noncomparable $\forall x\in A(x\preccurlyeq c\Rightarrow c=x)$ Hasse diagram: There are no lines downward from the element In the example $1$ is the maximal elements

Largest Element

Element $c$ of $A$ is the largest element of $A$ iff $\forall x\in A(x\preccurlyeq c)$ A largest element is always also maximal Note: largest element = greatest element = maximum Hasse diagram: There is a path downwards to all other elements In the example there is no largest element

Smallest Element

Element $c$ of $A$ is the smallest element of $A$ iff $\forall x\in A(c\preccurlyeq x)$ A smallest element is always also minimal Note: smallest element = least element = minimum Hasse diagram: There is a path upwards to all other elements In the example $1$ is the smallest element

Linearisation

Creating a Total Order Relations from a partial order, without violating the partial order relation Let $\preccurlyeq$ be a partial order on a set $A$. A linearisation of $\preccurlyeq$ is a total order ${\preccurlyeq }^{\ast }$ on $A$ such that $\forall x,y\in A(x\preccurlyeq y\Rightarrow x{\preccurlyeq }^{\ast }y)$

Example

For the “divides” relation on $\{1,2,3,9,18\}$ Linearisations will include:

• $1{\preccurlyeq }^{\ast }2{\preccurlyeq }^{\ast }3{\preccurlyeq }^{\ast }9{\preccurlyeq }^{\ast }18$
• $1{\preccurlyeq }^{\ast }3{\preccurlyeq }^{\ast }2{\preccurlyeq }^{\ast }9{\preccurlyeq }^{\ast }18$
• etc.

Kahn’s Algorithm

An algorithm that takes a finite set $A$ and a partial order $\preccurlyeq$ on $A$, and outputs a linearisation ${\preccurlyeq }^{\ast }$ of $\preccurlyeq$ Informally:

1. Find the a minimal element of $A$
2. Remove the element from $A$
3. Repeat until $A=\varnothing$
4. The linearisation is the elements that were removed, in the order of removal

Total Order Relations

If $R$ is a partial order relation on set $A$, and for any two elements $x$ and $y$ in $A$, either $xRy$ or $yRx$, then $R$ is a total order relation (or total order) on $A$ $R$ is a total order iff $R$ is a partial order and $\forall x,y\in A(xRy\vee yRx)$ Also called a linear order

Example

The $\le$ relation on $\mathbb{Q}$ is a total order because $\forall x,y\in \mathbb{Q}(x\le y\vee y\le x)$

Well-Ordered Set

Let $\preccurlyeq$ be a total order on a set $A$. $A$ is well-ordered iff every non-empty subset of $A$ contains a smallest element $\forall S\in \mathcal{P}(A),S\ne \varnothing \Rightarrow (\exists x\in S\forall y\in S(x\preccurlyeq y))$

Equivalence Relations

A relation is an equivalence relation iff it is reflexive, symmetric and transitive. $\sim$ is commonly used to denote an equivalence relation (it replaces $R$ in $aRb$, so $a\sim b$) This is the same as a partition, but from a different perspective

Equivalence Class

The equivalence class of an element is the component of the partition that contains the element e.g. Partition $\mathcal{C}=\{\{1,2,3\},\{4\}\}$, the equivalence class of $1$, denoted $[1]$ is $\{1,2,3\}$ Formally, Suppose $A$ is a set and $\sim$ is an equivalence relation on $A$. For each $a\in A$, the equivalence class of $a$, denoted $[a]$, called the class of $a$ for short, is the set of all elements $x\in A$ such that $a$ is $\sim$-related to $x$. Symbolically, $[a{]}_{\sim }=\{x\in A:a\sim x\}$

Lemma Rel.1 Equivalence Classes

Let $\sim$ be a equivalence relation on a set $A$. The following are equivalent for all $x,y\in A$.

• $x\sim y$
• $[x]=[y]$
• $[x]\cap [y]\ne \varnothing$

Set of equivalence classes

For set $A$ and equivalence relation $\sim$ on $A$, the set of all equivalence classes with respect to $\sim$ is denoted $A/\sim$ (“the quotient of $A$ by $\sim$“) $A/\sim =\{[x{]}_{\sim }:x\in A\}$ This is a partition of $A$ (Theorem Rel.2)

Theorem Rel.2

Equivalence classes form a partition Let $\sim$ be an equivalence relation on set $A$, then $A/\sim$ is a partition of $A$

Common Example: Congruence Relations

Congruence

Let $a,b\in \mathbb{Z}$ and $n\in {\mathbb{Z}}^{+}$ $a$ is congruent to $b$ modulo $n$ iff $n|(a-b)$ ($a-b$ is divisible by $n$) can be written as $a\equiv b\mathrm{mod}n$

Congruence Relation

Congruence modulo $n$ (mod-$n$) relation $R$: $\forall x,y\in \mathbb{Z}(xRy\iff n|(x-y))$
The quotient $\mathbb{Z}/{\sim }_n$ where ${\sim }_n$ is the congruence-mod-n relation on $\mathbb{Z}$ is denoted ${\mathbb{Z}}_n$

Properties

Congruence modulo $n$ relation is an Equivalence Relation, i.e. it splits the set of integers into partitions.

Divisibility

Definition

If $n$ and $d$ are integers and $d\ne 0$, then $n$ is divisible by $d$ iff $n$ equals $d$ times some integer

Notation

$d|n$ means ”$d$ divides $n$”, if $n,d\in \mathbb{Z}$ and $d\ne 0$ $d|n\iff \exists k\in \mathbb{Z}$ such that $n=dk$

Quotient-remainder Theorem

Given any integer $n$ and positive integer $d$, there exist unique integers $q$ and $r$ such that $n=dq+r$ and $0\le r<d$ $\frac{n}{d}=q$ , with remainder $r$

Example Use

let: $T_0=n\in \mathbb{Z}:n=3k\text{, for some integer }k,$ $T_1=n\in \mathbb{Z}:n=3k+1\text{, for some integer }k,$ $T_2=n\in \mathbb{Z}:n=3k+2\text{, for some integer }k$ Is $\{T_0,T_1,T_2\}$ a partition of $\mathbb{Z}$?

Yes. By the quotient-remainder theorem, every integer $n$ can be written in exactly one of the three forms: $n=3k$, $n=3k+1$, or $n=3k+2$ for some integer $k$. This means that $T_0,T_1,T_2$ are mutually disjoint and $\mathbb{Z}=T_0\cup T_1\cup T_2$