Connectives
- AND (conjunction): A B ; A B
- OR (disjunction): A + B ; A B
- NOT (negation): A’ ; ~A ;
Operator Precedence
From highest to lowest: Not (‘), And (), Or (+)
- A B’ + C = (A (B’)) + C
Laws
- Identity
- A + 0 = A
- A 1 = A
- Inverse/complement
- A + A’ = 1
- A A’ = 0
- Commutative
- A + B = B + A
- A B = B A
- Associative
- A + (B + C) = (A + C) + C
- A (B C) = (A B) C
- Distributive
- A (B + C) = (A B) + (A C)
- A + (B C) = (A + B) (A + C)
Theorems
- Idempotency
- X + X = X
- X X = X
- One element / zero element
- X + 1 = 1
- X 0 = 0
- Involution
- (X’)’ = X
- Absorption 1
- X + X Y = X
- X (X + Y) = X
- Absorption 2
- X + X’ Y = X + Y
- X (X’ + Y) = X Y
- DeMorgans’ (can be generalised to >2 variables)
- (X+Y)’ = X’ Y’
- (X Y)’ = X’ + Y’
- Consensus
- X Y + X’ Z + Y Z = X Y + X’ Z
- (X + Y) (X’ + Z) (Y + Z) = (X + Y) (X’ + Z)
Duality
- If AND/OR operators, and identity elements 0/1 in a boolean equation are interchanged, the equation remains valid
- if (x + y + z)’ = x’ y’ z’ is valid, then its dual, (x y z)’ = x’ + y’ + z’ is also valid
- if x + 1 = 1 is valid, then its dual x 0 = 0 is also valid
Boolean Functions
- A function that takes in boolean variables, and outputs a boolean value
- Complement functions: the complement F’ of a boolean function F, is obtained by swapping 1 and 0 in the function’s output values
- e.g. F = x y z’ , F’ = x’ + y’ + z (by DeMorgan’s and Involution)
Forms of boolean expressions
- Literal
- A variable on its own, or in its complemented form
- e.g. x , x’
- Product term
- A single literal, or several literals ANDed together
- e.g. x , x y z’
- Sum term
- A single literal, or several literals ORed together
- e.g. x , x + y + z’
- Sum of Products (SOP) expression
- A product term, or several product terms ORed together
- e.g. x , x + y z , x y’ + x z
- Product of Sum (POS) expression
- A sum term, or several sum terms ANDed together
- e.g. x , x (y + z’) , (x + y’) (x + z)
- Note: every boolean expression can be expressed in SOP or POS form
Minterm & Maxterm
- Minterm of n variables is a special product term that contains n literals from all the variables
- e.g. on 2 variables x and y, the minterms are x’ y’ , x’ y , x y’ and x y
- Maxterm of n variables is a special sum term that contains n literals from all the variables
- e.g. on 2 variables x and y, the maxterms are x + y , x + y’ , y’ + x and x’ + y’
- In general, with n variables, we have up to minterms and maxterms
- Each minterm is the complement of its maxterm, each maxterm is the complement of its minterm (e.g. m2’ = M2)
| x | y | minterm term | notation | maxterm term | notation |
|---|---|---|---|---|---|
| 0 | 0 | x’ y’ | m0 | x + y | M0 |
| 0 | 1 | x’ y | m1 | x + y’ | M1 |
| 1 | 0 | x y’ | m2 | x’ + y | M2 |
| 1 | 1 | x y | m3 | x’ + y’ | M3 |
Canonical/normal form
- A unique way of representing a boolean expression (each boolean expression only has one canonical form of each type)
- Types of canonical forms
- Sum-of-minterms (Canonical sum-of-products)
- Product-of-maxterms (Canonical product-of-sums)
- Sum of minterms
- Obtained by gathering the minterms of the function where the output is 1
- When x is 0, minterm will contain x’, when x is 1, minterm will contain x
- Can be expressed as a sum of ranges e.g. m(1, 3-5)
- Product of maxterms
- Obtained by gathering the maxterms of the function where the output is 0
- When x is 0, maxterm will contain x, when x is 1, maxterm will contain x’
- Can be expressed as a product of ranges e.g. M(0, 2, 6-7)
- Sum of minterms can be convert to product of maxterms and vice versa
- Convert by including the terms that were not included
- e.g. m(1, 3-5) → M(0, 2, 6-7)
- Can be proved by doing DeMorgan’s on F’
- Sum of minterms/product of maxterms of complement of F (F’) is found by including the terms that were not included
- e.g. F = m(1, 3-5) → F’ = m(0, 2, 6-7)
| x | y | F1 | F2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
- Sum of minterms
- F1 = x y’ = m2
- F2 = x’ y + x y = m(1,3)
- Product of maxterms
- F1 = (x + y) (x + y’) (x’ + y’) = M(0-1, 3)
- F2 = (x + y) (x’ + y) = M(0, 2)
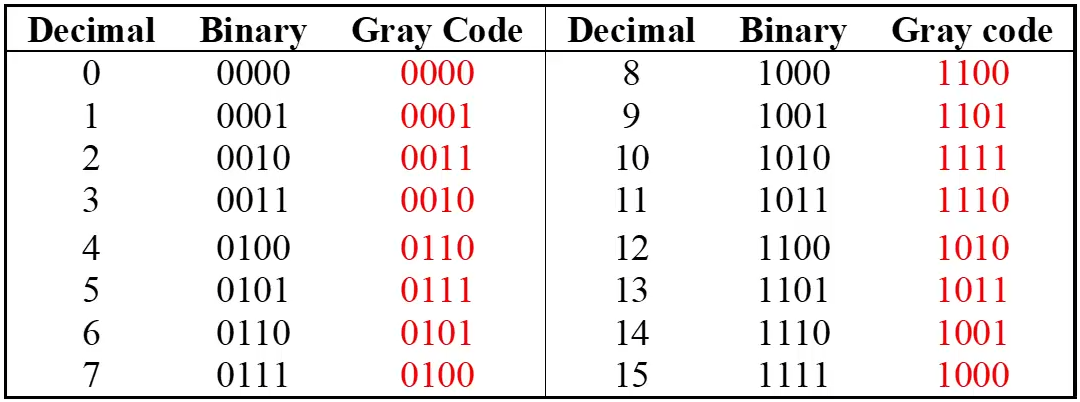
Gray Code
- also called reflected binary code
- Unweighted: each position does not mean a different thing (unlike binary, etc.)
- Only a single bit change from one code value to the next (including from the last value back to the first value)
- Not restricted to decimal digits: n bits → values
- Good for error detection
- Named after Frank Gray
- e.g. 4-bit standard gray code, generated by:
- First 2 values are always same as binary: 0000, 0001
- Next 2 values are generated by reflecting the first 2 values (0001, 0000), then changing the second bit to 1 (0011, 0010)
- Repeat by reflecting the first 4 values, and changing the third bit to 1 etc.
Simplification
- Simplification → fewer logic gates → cheaper, uses less power, sometimes faster
- Aims to minimise no. of literals and no. of terms
- Techniques
- Algebraic
- Karnaugh maps (k-maps) (max. 6 variables)
Algebraic Simplification
- Minimise no. of literals
- Use the laws/theorems to simplify the expression
K-maps
-
Systematic method to obtain sum of products
-
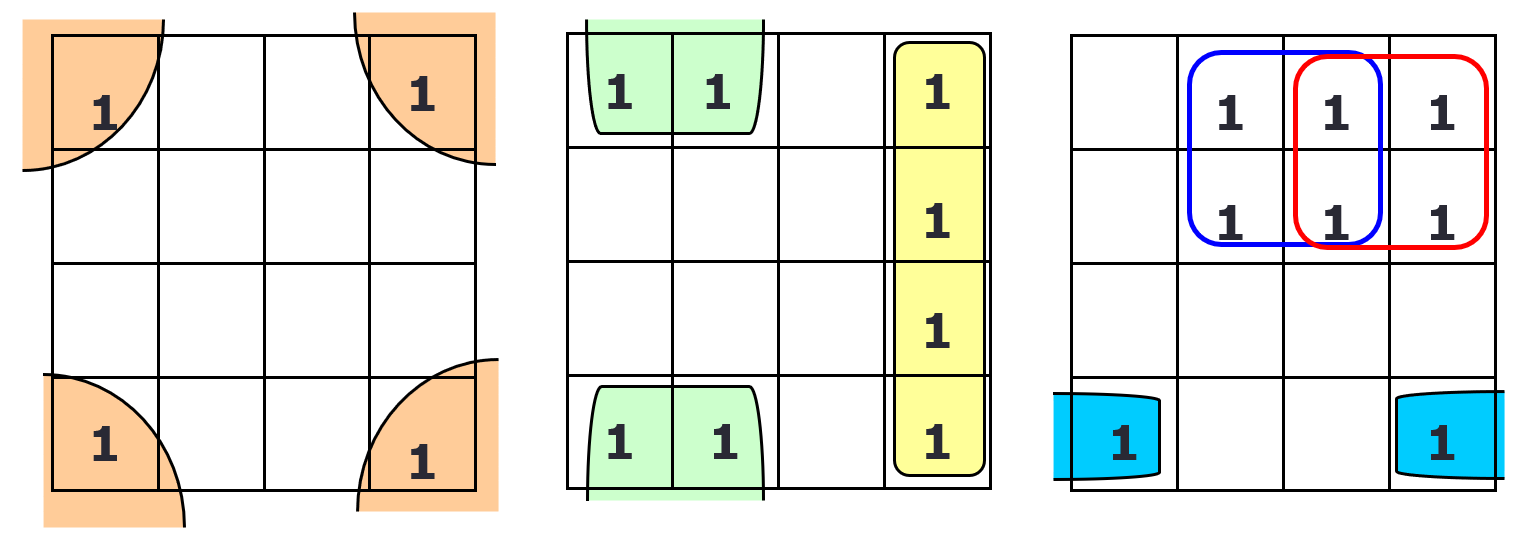
An abstract form of a Venn diagram, organised as a matrix of squares
- Each square represents a minterm
- Two adjacent squares represent minterms that differ by exactly one literal (axes with more than 1)
- Axes with more than 1 variables have to follow a grey code sequence
-
K-map sizes
- 2 variable: 2 by 2 square, with 1 variable on each axis (each cell has 2 neighbours)
- 3 variable: 2 by 4, with 2 variables on one axis, 1 variable on the other
- Each cell has 3 neighbours, so the long axis wraps around (if is horizontal rectangle, the leftmost cell wraps to the rightmost cell)
- 4 variable: 4 by 4, with 2 variables on each axis
- Each cell has 4 neighbours, so both axes wrap around
- 5 variable: two 4 by 4s, with two variables on each axis, and each of the 4 by 4s representing the last variable
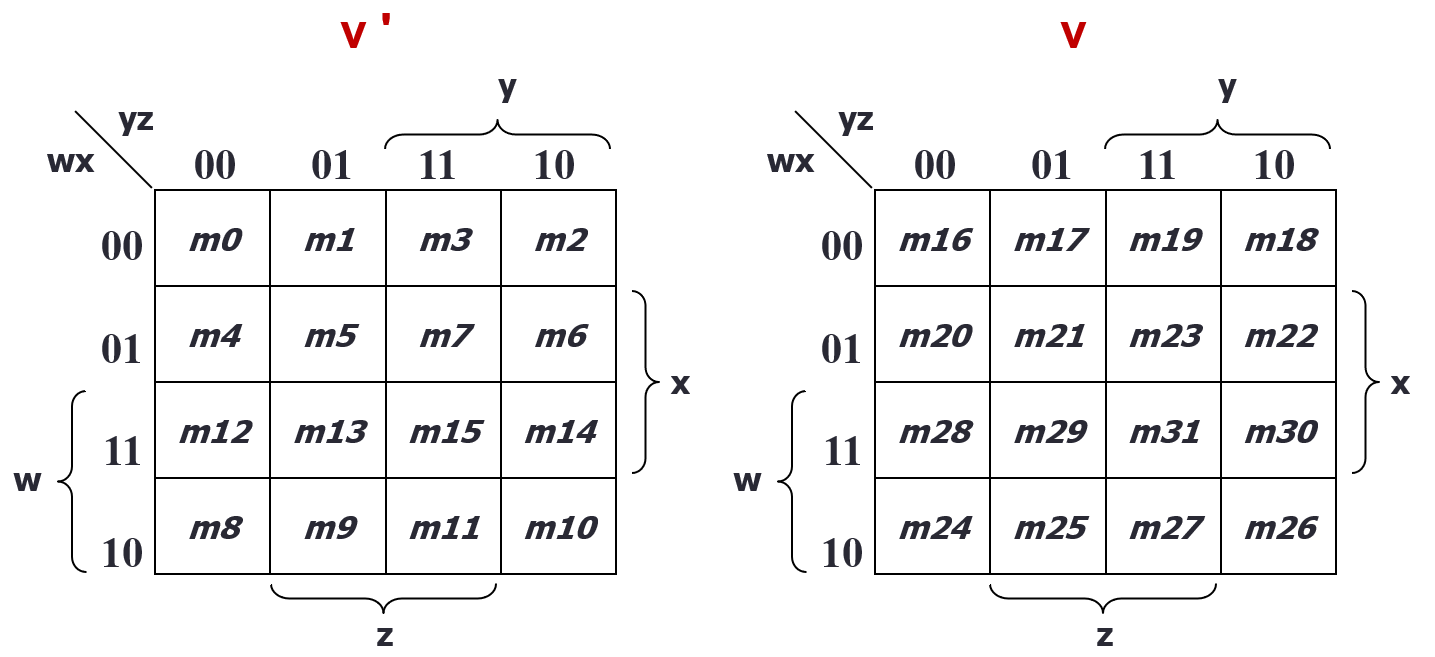
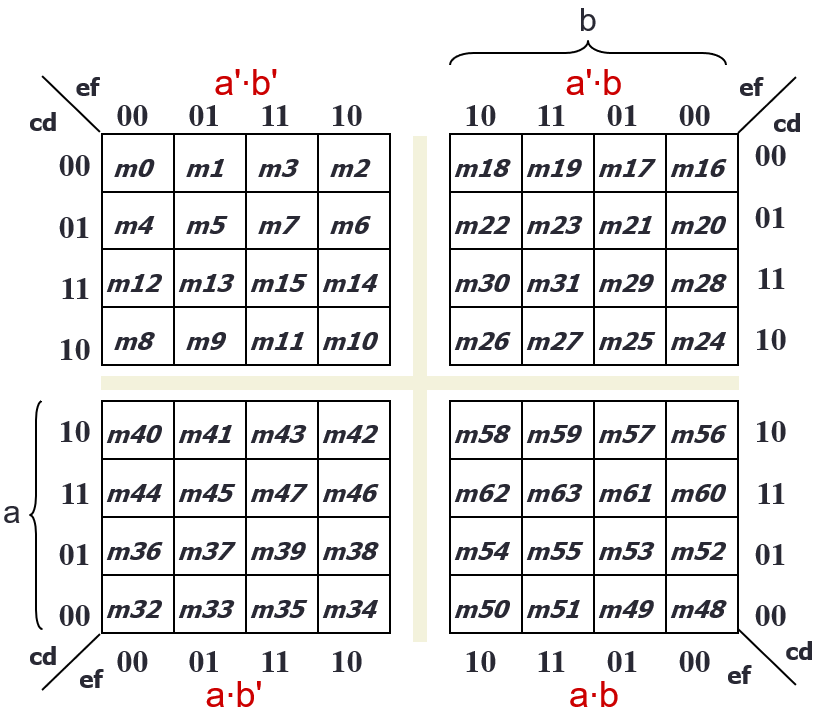
-
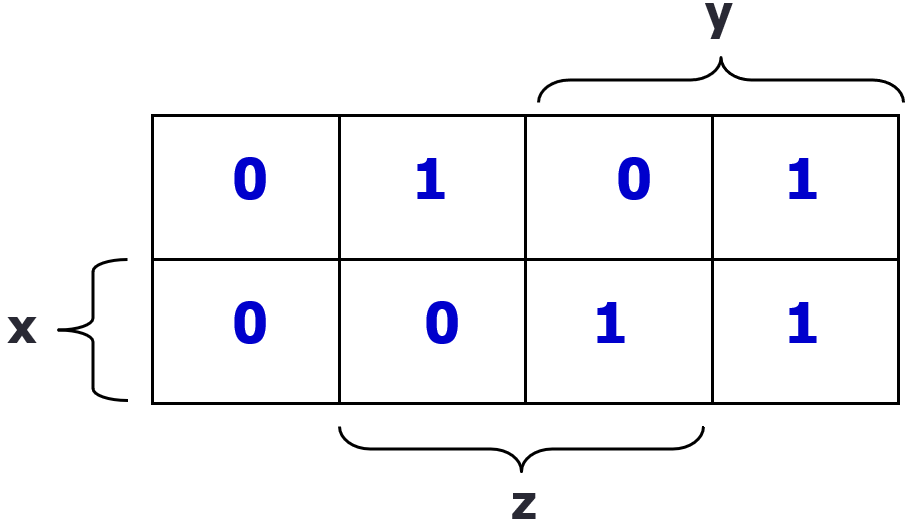
e.g. A(x, y, z) = x y + y z’ + x’ y’ z
- take the y z’ term, this means the cells that are “inside” the y region, and “outside” the z region are 1s
- after doing the above for all product terms, the remaining cells will be filled with zeros
-
How to use?
- Based on unifying theorem (complement law): A + A’ = 1
- Each cell corresponds to a minterm where the function output is 1
- Each valid grouping of adjacent cells containing 1 corresponds to a simpler product term of the function
- Group must have size in powers of 2: 1, 2, 4, 8…
- Grouping 2 adjacent cells eliminates 1 variable from the product term, grouping cells eliminates n variables
- Goal is to group as many cells as possible (maximise group size, or minimise number of groups)
- To find simplified POS expression, draw the k-map of F’, then find the SOP of F’. Then, find POS of F by negating both sides of the equation, and using DeMorgan’s
- F’ = SOP
- F = (SOP)’ = POS
- Don’t care conditions (where outputs can be either 1 or 0), denoted by X or d, usually when a certain combination of inputs are invalid (or will never occur)
- e.g. when the input is a half adder (the outputs C and S will never both be 1 at the same time)
- X can be chosen to be either 1 or 0, whichever will result in a simpler expression, check each X one by one to see if group size can be increased
- d(…) is used to denote the set of don’t care minterms
-
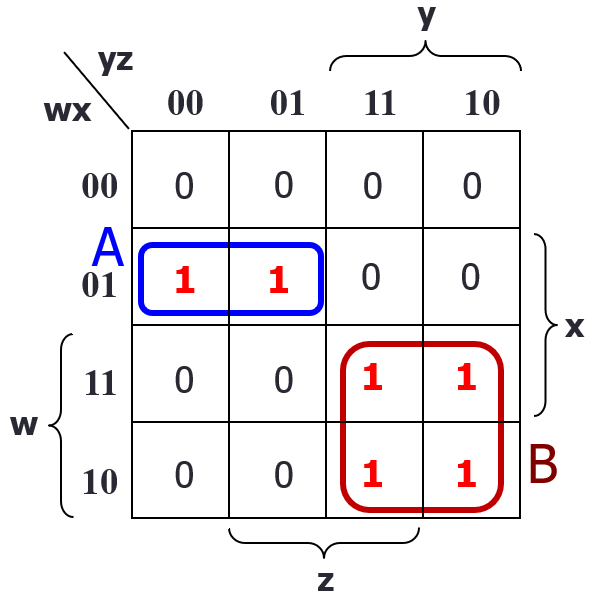
e.g. F(w, x, y, z) = w’ x y’ z’ + w’ x y’ z + w x’ y z’ + w x’ y z + w x y z’ + w x y z = m(4, 5, 10, 11, 14, 15)
- Write 1 in the corresponding minterm cells, or fill it in based on the sum of products (see the 3 variable k-map example above)
- Group the cells as much as possible
- Prime implicant (PI): made by combining the maximum possible adjacent cells (always do this, even if they overlap)
- Each PI should have at least one 1, cannot be all Xs
- Essential prime implicant (EPI): a PI that includes at least one minterm that is not covered by any other PI (i.e. do not form a group of cells of which all have already been grouped)
- To be considered covered by another PI, it is not necessary to be the same other PI
- Only count minterms that are 1, not X
- All groups have to be EPIs, this can be done by identifying all PIs and removing all non-essential PIs. If there are still cells not covered, select the minimum number of remaining PIs to cover the cells
- Prime implicant (PI): made by combining the maximum possible adjacent cells (always do this, even if they overlap)
- Simplify each group (remember that groups of cells will remove n terms)
- A = w’ x y’
- B = w y
- Combine simplified groups
- F(w, x, y, z) = w’ x y’ + w y
- F(w, x, y, z) = w’ x y’ + w y
Note: funny groups